Categories:
【转】一致性哈希 (Consistent Hashing)的前世今生
https://candicexiao.com/consistenthashing/
一致性哈希是一种特殊的哈希,主要的应用场景是:当我们的服务是一个有状态服务等时候,需要根据特定的KEY路由到相同的目标服务机器进行处理的场景。 本文首先将从哈希本身开始讨论,然后讨论分布式哈希及面对的问题,从而引入一致性哈希如何解决这些问题;在最后一章还将讨论一致性哈希的其他算法和发展。
一致性哈希是一种特殊的哈希,主要的应用场景是:当我们的服务是一个有状态服务等时候,需要根据特定的key路由到相同的目标服务机器进行处理的场景。
一致性哈希的概念在 Karger 1997年发布的论文 《一致的哈希和随机树:缓解万维网上的热点的分布式缓存协议》 中引入,之后在许多其他分布式系统(如Cassandra,Riak等)中使用,并不断优化和改良。
本文首先将从哈希本身开始讨论,然后讨论分布式哈希及面对的问题,从而引入一致性哈希如何解决这些问题;在最后一章还将讨论一致性哈希的其他算法和发展。
二、一致性哈希是为了解决什么问题?
2.1 什么是Hash
Hash是将一个数据(通常是任意大小的对象)映射到另一固定大小的数据(通常是整数,称为哈希码或简称hash)的过程。把将某数据映射到哈希码的这个函数hash(),称为哈希函数。
例如,哈希函数可用于将随机大小的字符串映射到0到N之间的某个固定整数数字。
hello ---> 60
hello world ---> 40
可能会有字符串映射到相同的整数的场景,被称为碰撞。
处理碰撞的常见解决方案是 链式 和 开放式寻址。
注:
- 开放定址法:一旦发生了冲突,就去寻找下一个空的散列地址,只要散列表足够大,空的散列地址总能找到,并将记录存入。 – 链式(常用):将哈希表的每个单元作为链表的头结点,所有哈希地址为i的元素构成一个同义词链表。即发生冲突时就把该关键字链在以该单元为头结点的链表的尾部。
2.2 我们的场景
目前有一个有状态的缓存服务,服务需要缓存n位员工的email信息到姓名的映射:john@example.com 张三,mark@example.com 李四 … ,在访问时,我们需要对其做增删查
2.2.1存储方式对比
根据上面的场景,我们可以考虑以下的数据结构:
- 数组 每个操作的最坏情况时间复杂度将为O(n)。通过存储排序的数据并使用二分查找,可以将搜索优化为O(logn)
- 链表 如果我们将使用链接列表存储员工记录,则最坏情况下的插入时间为O(1),搜索和删除时间为O(n)
- 二叉搜索树(Binary Search Tree) 每个操作的最坏情况时间将为O(log n)
- 哈希函数+数组 使用哈希函数可用于将对象key(即email)哈希为固定大小的整数。然后我们可以使用数组下标i作为哈希结果,存储员工详细信息。 但考虑到哈希函数的散列范围大,使用数组下标需要创建一个大数组,会非常浪费内存。
- 哈希函数+哈希表 使用哈希表可以解决这个问题,哈希表使用固定大小的N数组来映射所有键的哈希码。 假设我们是对key哈希再取模获取数组索引:index = hash(key) mod N 由于可能有多个key映射到同一索引,因此每个索引都将附加一个列表或存储桶bucket,以存储映射到同一索引的所有对象。
所以方案5使用哈希表是一个很好的方案,由于哈希函数为O(1)复杂度,如果哈希表的大小得当,每个存储桶的数量较少,那么访问的速度很快。
2.3 分布式哈希
考虑在刚才的场景下,如果员工数量大大增长,存储在一台计算机上的哈希表中变得困难。
在这种情况下,我们希望能够将哈希表分发到多个服务器,避免单台服务器的限制。所以我们需要使key尽量均匀的分布在多个服务器。
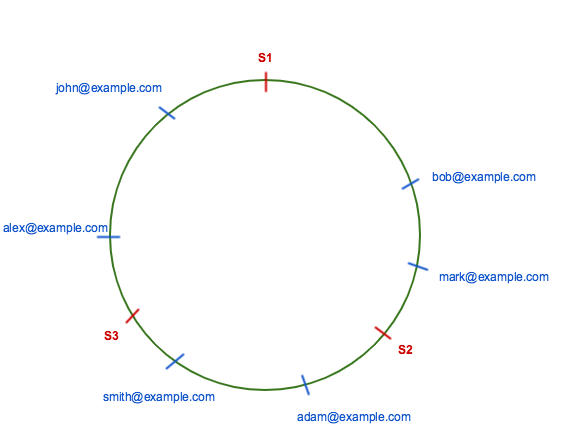
最常见的方法是hash取模:
server = hash(key)mod 3 //假设后端有3个服务器
三个服务器分别是S1,S2和S3,示例结果如下:
john@example.com 89 2(S3)
mark@example.com 30 0(S1)
adam@examle.com 47 2(S3)
smith@example.com 52 1(S2)
alex@example.com 75 0(S0)
bob@example.com 22 1(S2)
2.3.1 分布式哈希存在的问题
重新哈希问题
假设其中一台服务器(S3)崩溃了,它不再能够接受请求。现在我们只剩下两台服务器了。几乎所有密钥的服务器位置都已更改,不仅是S3中的密钥。
对后端真实服务器来说,将大大增加服务器的负载(因为会丢失缓存后需要重新查询建立映射)。
对客户端来说,并且由于映射方式的改变大量mail都被映射到新的服务器上,导致映射在这一刻都不可用。这个问题被称为重新哈希问题。
john@example.com 89 1(S2)
mark@example.com 30 0(S1)-
adam@examle.com 47 1(S2)
smith@example.com 52 0(S1)
alex@example.com 75 1(S2)
bob@example.com 22 0(S1)
所以 我们需要一个一致性哈希算法
一致性哈希是一种分布式哈希方案,使服务器的伸缩不会给整个系统带来大问题。
三、经典一致性哈希
2.1 一致性哈希的目标
1997年,Karger等人发布了论文 《Consistent Hashing and Random Trees: Distributed Caching Protocols for Relieving Hot Spots on the WWW》 ,并提出了一致性哈希
在论文中还对一致性哈希的算法好坏定义给出了4个评判指标:
评判指标
- 平衡性(Balance) 不同key的哈希结果分布均衡,尽可能的均衡地分布到各节点上。平衡性跟哈希函数关系密切,目前许多哈希算法都有较好的平衡性。
- 单调性(Monotonicity) 当有新的节点上线后,系统中原有的key要么还是映射到原来的节点上,映射到新加入的节点上,不会出现从一个老节点重新映射到另一个老节点。即表示:当可用存储桶的集合发生更改时,只有在必要时才移动项目以保持均匀的分布。
- 分散性(Spread) 由于客户端可能看不到后端的所有服务,这种情况下对于固定的key,在两个客户端上可能被分散到不同的后端服务,从而降低后端存储的效率,所以算法应该尽量降低分散性。
- 服务器负载均衡(Load) 负载主要是从服务器的角度来看,指各服务器的负载应该尽量均衡
2.2 算法思路
Karger等人在后续的论文 《Web caching with consistent hashing》 中提出了一致性哈希的实现,也就是大家常称的环割法。
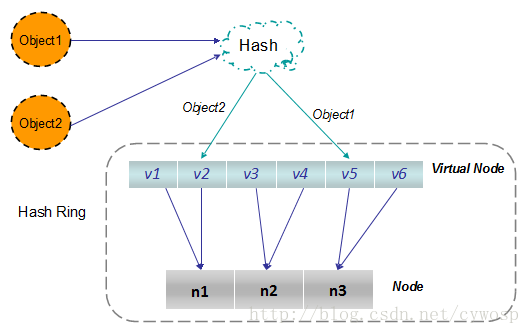
2.2.1 一致性哈希思路
- 我们把节点通过hash后,映射到一个范围是[0,2^32]的环上
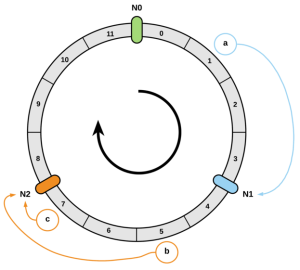
- 把数据也通过hash的方式映射到环上
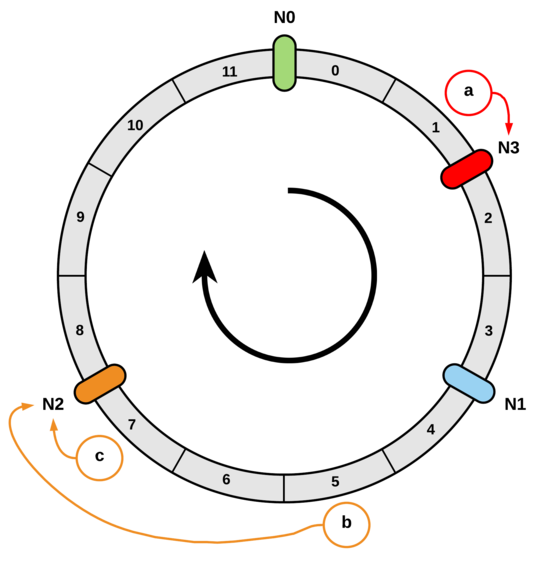
- 然后按顺时针方向查找第一个hash值大于等于数据的hash值的节点,该节点即为数据所分配到的节点。
可优化点:
当删除服务器S3时,存在一个问题,即来自S3的密钥没有在其余服务器S1和S2之间平均分配
理论的情况,从n个服务器扩容到n+1时,只需要重新映射1/ n+1的key
2.1.2 均衡性优化 - 引入虚拟节点
因为节点越多,它们在环上的分布就越均匀,使用虚拟节点还可以降低节点之间的负载差异
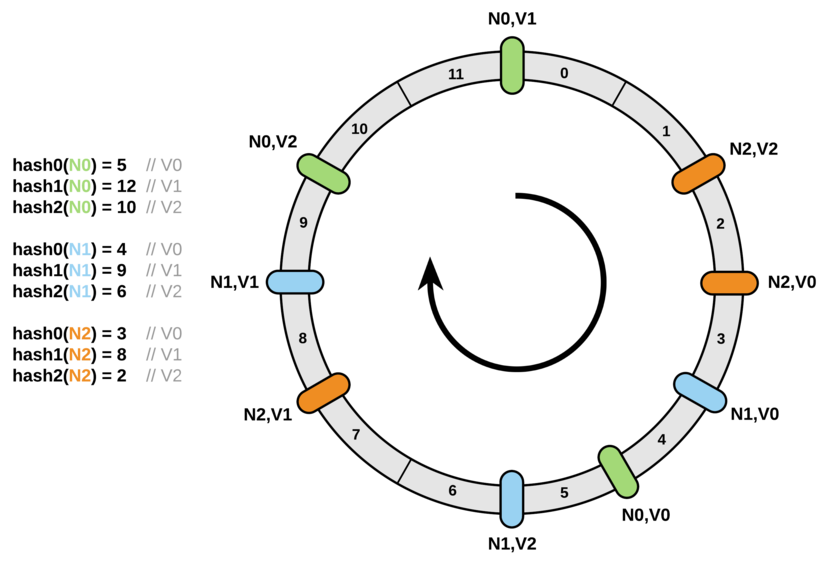
查找时如下:
2.2.2 算法特点
- 哈希环需要占用客户端内存,具体大小根据节点(虚拟节点)的个数确定
2.2 算法具体实现
2.2.1 ketama 算法
ketama 算法是最常用的一种一致性哈希算法的实现,广泛应用在存储及各rpc产品中,如memcache、redis,nginx、envoy等。github上面有 Ketama的多语言实现 的代码
算法核心思路
从配置文件中读取服务器节点列表,包括节点的地址及mem,其中mem参数用来衡量一个节点的权重
对每个节点按权重计算需要生成几个虚拟节点,基准是每个节点160个虚拟节点,每个节点会生成10.0.1.1:11211-1、10.0.1.1:11211-2到10.0.1.1:11211-40共40个字符串,并以此算出40个16字节的hash值(其中hash算法采用的md5),每个hash值生成4个4字节的hash值,总共40*4=160个hash值,对应160个虚拟节点
把所有的hash值及对应的节点地址存到一个continuum存组中,并按hash值排序方便后续二分查找计算数据所属节点
核心代码
#服务器节点例子,第一列为地址,第二列为权重
#------ Server ------- -Mem-#
#255.255.255.255:65535 66666#
10.0.1.1:11211 600
10.0.1.2:11211 300
10.0.1.3:11211 200
10.0.1.4:11211 350
10.0.1.5:11211 1000
10.0.1.6:11211 800
10.0.1.7:11211 950
10.0.1.8:11211 100
typedef struct
{
unsigned int point; // point on circle
char ip[22];
} mcs;
typedef struct
{
char addr[22];
unsigned long memory;
} serverinfo;
typedef struct
{
int numpoints;
void* modtime;
void* array; //array of mcs structs
} continuum;
typedef continuum* ketama_continuum;
/** \brief Generates the continuum of servers (each server as many points on a circle).
* \param key Shared memory key for storing the newly created continuum.
* \param filename Server definition file, which will be parsed to create this continuum.
* \return 0 on failure, 1 on success. */
static int
ketama_create_continuum( key_t key, char* filename )
{
if (shm_ids == NULL) {
init_shm_id_tracker();
}
if (shm_data == NULL) {
init_shm_data_tracker();
}
int shmid;
int* data; /* Pointer to shmem location */
unsigned int numservers = 0;
unsigned long memory;
serverinfo* slist;
slist = read_server_definitions( filename, &numservers, &memory );
/* Check numservers first; if it is zero then there is no error message
* and we need to set one. */
if ( numservers < 1 )
{
set_error( "No valid server definitions in file %s", filename );
return 0;
}
else if ( slist == 0 )
{
/* read_server_definitions must've set error message. */
return 0;
}
#ifdef DEBUG
syslog( LOG_INFO, "Server definitions read: %u servers, total memory: %lu.\n",
numservers, memory );
#endif
/* Continuum will hold one mcs for each point on the circle: */
mcs continuum[ numservers * 160 ];
unsigned int i, k, cont = 0;
for( i = 0; i < numservers; i++ )
{
float pct = (float)slist[i].memory / (float)memory;
// 按内存权重计算每个物理节点需要分配多少个虚拟节点,正常是160个
unsigned int ks = floorf( pct * 40.0 * (float)numservers );
#ifdef DEBUG
int hpct = floorf( pct * 100.0 );
syslog( LOG_INFO, "Server no. %d: %s (mem: %lu = %u%% or %d of %d)\n",
i, slist[i].addr, slist[i].memory, hpct, ks, numservers * 40 );
#endif
for( k = 0; k < ks; k++ )
{
/* 40 hashes, 4 numbers per hash = 160 points per server */
char ss[30];
unsigned char digest[16];
// 在节点的addr后面拼上个序号,然后以该字符串去计算hash值
sprintf( ss, "%s-%d", slist[i].addr, k );
ketama_md5_digest( ss, digest );
/* Use successive 4-bytes from hash as numbers
* for the points on the circle: */
int h;
// 16字节,每四个字节作为一个虚拟节点的hash值
for( h = 0; h < 4; h++ )
{
continuum[cont].point = ( digest[3+h*4] << 24 )
| ( digest[2+h*4] << 16 )
| ( digest[1+h*4] << 8 )
| digest[h*4];
memcpy( continuum[cont].ip, slist[i].addr, 22 );
cont++;
}
}
}
free( slist );
// 排序,方便二分查找
/* Sorts in ascending order of "point" */
qsort( (void*) &continuum, cont, sizeof( mcs ), (compfn)ketama_compare );
. . .
return 1;
}
算法评价
优点:
- 满足单调性
- 复杂度:算法复杂度为log(vn);其中n为节点数,v为每个节点的虚拟节点数(默认160)
- 应用广泛:实现简单,广泛被使用
缺点:
- 占用内存较大:内存占用v*n
- 虚拟节点数少的情况下,平衡性较差
四、其他几种一致性哈希算法
4.1 集合哈希(Rendezvous hashing)/ 最高随机权重哈希 (HRW)
集合哈希,也叫最高随机权重哈希(HRW) , 是一种算法,1996年的论文 《A Name-Base Mapping Scheme for Rendezvous》 中发布,让多个客户端对各key映射到后端ñ个服务达成共识。一个典型的应用是客户需要将对象分配给哪些站点(或代理)达成一致。
4.1.1 算法思路
计算一个key应该放入到哪个S时,使用哈希函数h(key,S)计算每个候选S的值,然后返回值最大的S。
示例代码
其中nodes是一个数组,其内容可以是数字索引,也可以是ip,用来表示server。给定nodes和key,就会返回key所对应的节点。
function hrw_hash( nodes, key )
local entries = {}
for k,v in pairs(nodes) do
entries[#entries + 1] = {node=v, weight=mmh3.hash32(tostring(key),v)}
end
local max_weight = 1
local max_node = 0
local max_index = 0
for k,v in pairs(entries) do
if v.weight > max_weight then
max_weight = v.weight
max_node = v.node
max_index = k
end
end
return max_node, max_index
end
4.1.2 特点
- 负载均衡:由于散列函数随机化,并且可加权重:具有不同容量的站点可以在站点列表中与容量成比例地表示。
- 高命中率:由于所有在客户端上对key映射是一样的。除非是替换hash算法等,总是会命中对应的S。
- 节点S变动导致的干扰小:当站点Sn发生故障时,只是需要重新映射到原映射到该站点的对象。如所证明的,中断处于最小可能的级别。
4.1.3 适合场景
- 经典一致性哈希需要存储,HRW不需要预先存储
- 适合S个数少的情况,S比较多的时候耗时也较长,算法复杂度为O(n)
4.1.4 复杂度改良
针对S较多的场景,有人提出了改进的方法:Skeleton-based variant
将S组织成tree的结构:假设我们有108个节点,选择一个常数m(图中是4),计算出c=108/4=27组节点,构成一个树
如图找到组节点后,再计算出真实节点的hash并选择最大的那个,即为访问结果。
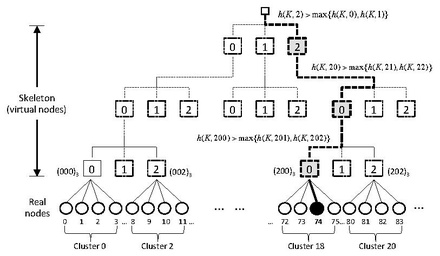
优缺点分析:
复杂度为O(logn),缺点是扩缩容后,在reblance的时候花费时间较长。
4.2 跳转一致性哈希(Jump consistent hash)
Jump consistent hash是Google于2014年发表的论文 《A Fast, Minimal Memory, Consistent Hash Algorithm》 中提出的一种一致性哈希算法,它占用内存小且速度很快,并且只有大概5行代码,比较适合用在分shard的分布式存储系统中,在Google的java库guava等有应用。
4.2.1 算法目标
平衡性:对象均匀分布
单调性:bucket的数量变化时,只需把少部分旧对象移到新桶。
4.2.2 算法思路
实例数从n变化到n+1后,ch(k,n+1) 的结果中,应该有占比 n/(n+1) 的结果保持不变,而有 1/(n+1) 跳变为 n+1。
所以我们可以通过[0,1]区间的key做随机种子的随机变量,来决定当次是否跳变,最终返回最后一次跳变的结果。
int ch(int key, int num_buckets) {
random.seed(key) ;
int b = 0; // b will track ch(key, j +1) .
for (int j = 1; j < num_buckets; j ++) {
if (random.next() < 1.0/(j+1) ) b = j ;
}
return b;
}
这个算法是O(n)的,仔细观察会发现,随着j增大,随机数小于1/(j+1)的概率很小,所以作者引入了一个随机数r,通过r得到了j。将代码复杂度进行了改进:
int ch(int key, int num_buckets) {
random. seed(key) ;
int b = -1; // bucket number before the previous jump
int j = 0; // bucket number before the current jump
while(j<num_buckets){
b=j;
double r=random.next(); // 0<r<1.0
j = floor( (b+1) /r);
}
return b;
}
算法复杂度:可以假设每次r都取0.5,则可以认为每次 j=2*j,因此时间复杂度为O(log(n))。
4.2.3 算法完整代码
采用适当的随机数算法(使用线性同余方法产生随机数,原理可阅读一份Jump Hash的讨论)后,完整的代码如下,其输入是一个64位的key及桶的数量,输出是返回这个key被分配到的桶的编号。
int32_t JumpConsistentHash(uint64_t key, int32_t num_buckets) {
int64_t b = -1, j = 0;
while (j < num_buckets) {
b = j;
key = key * 2862933555777941757ULL + 1;
j = (b + 1) * (double(1LL << 31) / double((key >> 33) + 1));
}
return b;
}
4.2.4 算法性能
执行耗时
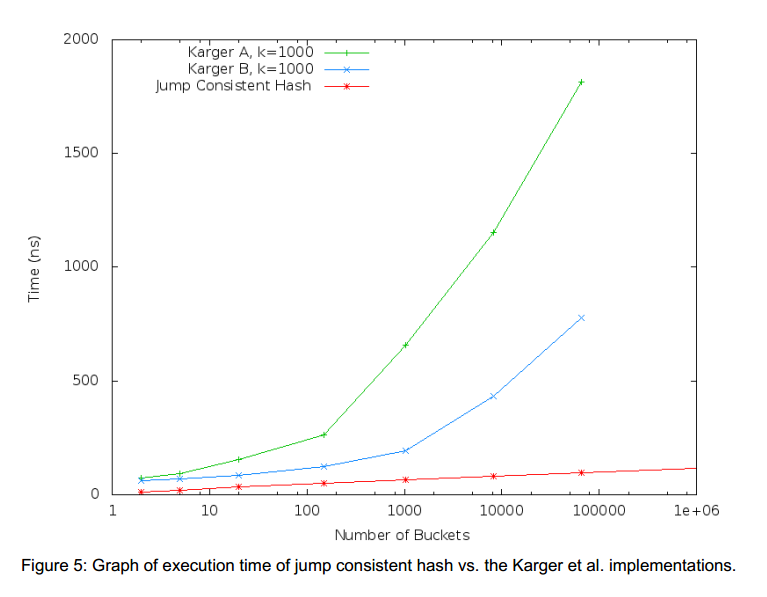
与Karger的算法对比:其中A是使用map来存储节点,B使用排序后的数组来存储映射,查找时使用二分查找
4.2.5 算法特点
优点:
- 无需存储虚拟节点
- 性能强
- 结果分布的均匀性与key分布无关,由伪随机数生成器的均匀性保证
- 复杂度为log(n)
缺点:
- 由于算法特性,后台节点id需要是有序的int,或者管理好节点id
- 对于中间和多个节点剔除的情况,数据仍会落到原节点,需要额外处理(主备、doublehash或管理好节点id)
4.3 有界载荷一致性哈希 Consistent Hashing with Bounded Loads
4.3.1 背景
当一致性hash的key本身不均匀时,比如:某些内容比其他内容(如互联网上的常用内容)更受欢迎,一致hash会将对该流行内容的所有请求发送到同一服务器子集,这将带来比其他服务器多得多的流量。
这可能会导致服务器过载,视频播放质量差以及用户不满意(分段缓存的场景)。
Google在2017年发布论文《Consistent Hashing and Random Trees:Distributed Caching Protocols for Relieving Hot Spots on the www》和博客讨论了这种场景下,对一致性哈希改良
4.3.2 目标
当服务器伸缩后,最大程度地减少之后的移动次数,并且最大程度地减少任何服务器的最大负载
4.3.3 思路
假设有m个请求和n个服务 定义c = 1+ε > 1
定义容量capacity = cm/n 如1.25
4.3.4算法思路
想象一个给定范围的数字,它覆盖在一个圆上。顺时针移动时,分配给第一个非满负载料箱(如果节点负载达到1.25会跳过该节点)。
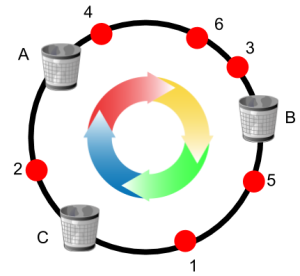
该算法略微降低了一致性(具体降低的程度与 ε 的设置有关),但后台服务的负载较均衡性得到了提高。
4.4 悬浮一致性哈希 Maglev Hash
通过提前建立查找表,复杂度为O(1)
没有做最小化重新映射,适合后端节点数万级的场景
参考:Google2016年发布的论文 Maglev: A Fast and Reliable Software Network Load Balancer
参考与引用
Consistent Hashing: Algorithmic Tradeoffs - Damian Gryski from Medium